Find the Solutions to 9x 2-63x 0
Systems of Linear and Quadratic Equations
A System of those two equations can be solved (find where they intersect), either:
- Graphically (by plotting them both on the Function Grapher and zooming in)
- or using Algebra
How to Solve using Algebra
- Make both equations into "y =" format
- Set them equal to each other
- Simplify into "= 0" format (like a standard Quadratic Equation)
- Solve the Quadratic Equation!
- Use the linear equation to calculate matching "y" values, so we get (x,y) points as answers
An example will help:
Example: Solve these two equations:
- y = x2 - 5x + 7
- y = 2x + 1
Make both equations into "y=" format:
They are both in "y=" format, so go straight to next step
Set them equal to each other
x2 - 5x + 7 = 2x + 1
Simplify into "= 0" format (like a standard Quadratic Equation)
Subtract 2x from both sides: x2 - 7x + 7 = 1
Subtract 1 from both sides: x2 - 7x + 6 = 0
Solve the Quadratic Equation!
(The hardest part for me)
You can read how to solve Quadratic Equations, but here we will factor the Quadratic Equation:
Start with: x2 - 7x + 6 = 0
Rewrite -7x as -x-6x: x2 - x - 6x + 6 = 0
Then: x(x-1) - 6(x-1) = 0
Then: (x-1)(x-6) = 0
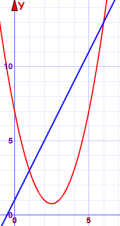
Which gives us the solutions x=1 and x=6
Use the linear equation to calculate matching "y" values, so we get (x,y) points as answers
The matching y values are (also see Graph):
- for x=1: y = 2x+1 = 3
- for x=6: y = 2x+1 = 13
Our solution: the two points are (1,3) and (6,13)
I think of it as three stages:
Combine into Quadratic Equation ⇒ Solve the Quadratic ⇒ Calculate the points
Solutions
There are three possible cases:
- No real solution (happens when they never intersect)
- One real solution (when the straight line just touches the quadratic)
- Two real solutions (like the example above)

Time for another example!
Example: Solve these two equations:
- y - x2 = 7 - 5x
- 4y - 8x = -21
Make both equations into "y=" format:
First equation is: y - x2 = 7 - 5x
Add x2 to both sides: y = x2 + 7 - 5x
Second equation is: 4y - 8x = -21
Add 8x to both sides: 4y = 8x - 21
Divide all by 4: y = 2x - 5.25
Set them equal to each other
x2 - 5x + 7 = 2x - 5.25
Simplify into "= 0" format (like a standard Quadratic Equation)
Subtract 2x from both sides: x2 - 7x + 7 = -5.25
Add 5.25 to both sides: x2 - 7x + 12.25 = 0
Solve the Quadratic Equation!
Using the Quadratic Formula from Quadratic Equations:
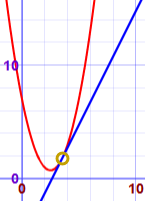
- x = [ -b ± √(b2-4ac) ] / 2a
- x = [ 7 ± √((-7)2-4×1×12.25) ] / 2×1
- x = [ 7 ± √(49-49) ] / 2
- x = [ 7 ± √0 ] / 2
- x = 3.5
Just one solution! (The "discriminant" is 0)
Use the linear equation to calculate matching "y" values, so we get (x,y) points as answers
The matching y value is:
- for x=3.5: y = 2x-5.25 = 1.75
Our solution: (3.5,1.75)
Real World Example
Kaboom!
The cannon ball flies through the air, following a parabola: y = 2 + 0.12x - 0.002x2
The land slopes upward: y = 0.15x
Where does the cannon ball land?
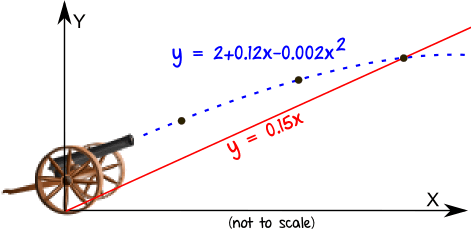
Both equations are already in the "y =" format, so set them equal to each other:
0.15x = 2 + 0.12x - 0.002x2
Simplify into "= 0" format:
Bring all terms to left: 0.002x2 + 0.15x - 0.12x - 2 = 0
Simplify: 0.002x2 + 0.03x - 2 = 0
Multiply by 500: x2 + 15x - 1000 = 0
Solve the Quadratic Equation:
Split 15x into -25x+40x: x2 -25x + 40x - 1000 = 0
Then: x(x-25) + 40(x-25) = 0
Then: (x+40)(x-25) = 0
x = -40 or 25
The negative answer can be ignored, so x = 25
Use the linear equation to calculate matching "y" value:
y = 0.15 x 25 = 3.75
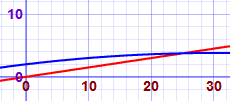
So the cannonball impacts the slope at (25, 3.75)
You can also find the answer graphically by using the Function Grapher:
 .
.
Both Variables Squared
Sometimes BOTH terms of the quadratic can be squared:
Example: Find the points of intersection of
The circle x2 + y2 = 25
And the straight line 3y - 2x = 6
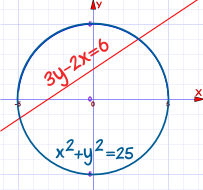
First put the line in "y=" format:
Move 2x to right hand side: 3y = 2x + 6
Divide by 3: y = 2x/3 + 2
NOW, Instead of making the circle into "y=" format, we can use substitution (replace "y" in the quadratic with the linear expression):
Put y = 2x/3 + 2 into circle equation: x2 + (2x/3 + 2)2 = 25
Expand: x2 + 4x2/9 + 2(2x/3)(2) + 22 = 25
Multiply all by 9: 9x2 + 4x2 + 2(2x)(2)(3) + (9)(22) = (9)(25)
Simplify: 13x2+ 24x + 36 = 225
Subtract 225 from both sides: 13x2+ 24x - 189 = 0
Now it is in standard Quadratic form, let's solve it:
13x2+ 24x - 189 = 0
Split 24x into 63x-39x: 13x2+ 63x - 39x - 189 = 0
Then: x(13x + 63) - 3(13x + 63) = 0
Then: (x - 3)(13x + 63) = 0
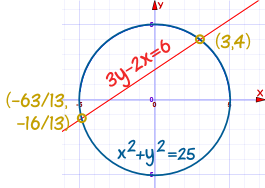
So: x = 3 or -63/13
Now work out y-values:
Substitute x = 3 into linear equation:
- 3y - 6 = 6
- 3y = 12
- y = 4
- So one point is (3, 4)
Substitute x = -63/13 into linear equation:
- 3y + 126/13 = 6
- y + 42/13 = 2
- y = 2 - 42/13 = 26/13 - 42/13 = -16/13
- So the other point is (-63/13, -16/13)
Find the Solutions to 9x 2-63x 0
Source: https://www.mathsisfun.com/algebra/systems-linear-quadratic-equations.html